The Thigh High Socks With the 3 Lines and Trasparent Sections Between the Lines

Different words, same formula

Example One

The slope of a line going through the point (1, 2) and the point (4, 3) is $$ \frac{1}{3}$$.

Remember: difference in the y values goes in the numerator of formula, and the difference in the x values goes in denominator of the formula.

Can either point be $$( x_1 , y_1 ) $$ ?

There is only one way to know!

The work , side by side

point (4, 3) as $$ (x_1, y_1 )$$

$$ slope = \frac{y_{2}-y_{1}}{x_{2}-x_{1}} = \frac{3-2}{4-1} = \frac{1}{3} $$

point (1, 2) as $$ (x_1, y_1 )$$

$$ slope = \frac{y_{2}-y_{1}}{x_{2}-x_{1}} = \frac{2-3}{1-4} = \frac{-1}{-3} = \frac{1}{3} $$

Answer: It does not matter which point you put first. You can start with (4, 3) or with (1, 2) and, either way, you end with the exact same number! $$ \frac{1}{3} $$

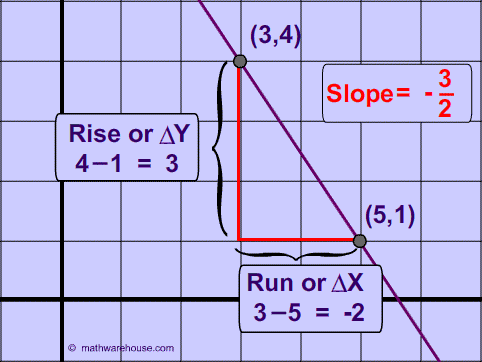
Example 2 of the Slope of A line

The slope of a line through the points (3, 4) and (5, 1) is $$- \frac{3}{2}$$ because every time that the line goes down by 3(the change in y or the rise) the line moves to the right (the run) by 2.

Video Tutorial on the Slope of a Line

Slope of vertical and horizontal lines

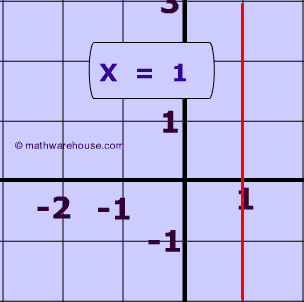
The slope of a vertical line is undefined

This is because any vertical line has a $$\Delta x$$ or "run" of zero. Whenever zero is the denominator of the fraction in this case of the fraction representing the slope of a line, the fraction is undefined. The picture below shows a vertical line (x = 1).

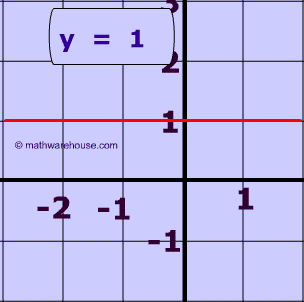
The slope of a horizontal line is zero

This is because any horizontal line has a $$\Delta y$$ or "rise" of zero. Therefore, regardless of what the run is (provided its' not also zero!), the fraction representing slope has a zero in its numerator. Therefore, the slope must evaluate to zero. Below is a picture of a horizontal line -- you can see that it does not have any 'rise' to it.

Do any two points on a line have the same slope?

Answer: Yes, and this is a fundamental point to remember about calculating slope.

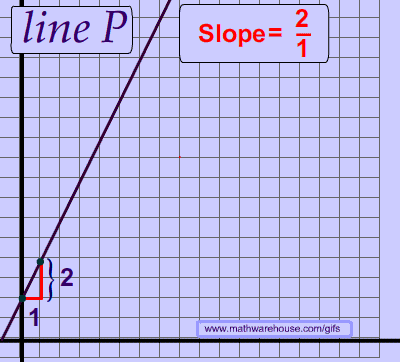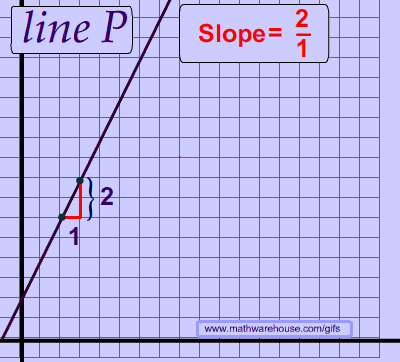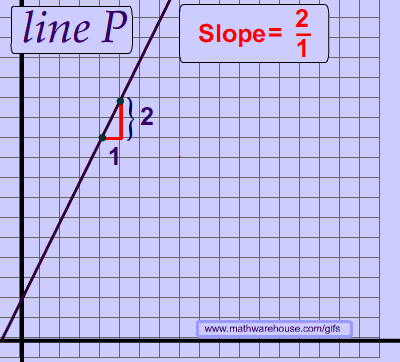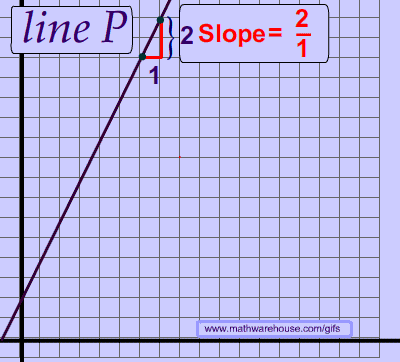
Every line has a consistent slope. In other words, the slope of a line never changes. This fundamental idea means that you can choose any 2 points on a line.

Think about the idea of a straight line. If the slope of a line changed, then it would be a zigzag line and not a straight line, as you can see in the picture above.

As you can see below, the slope is the same no matter which 2 points you chose.

The Slope of a Line Never Changes

Practice Problems

Problem 1

What is the slope of a line that goes through the points (10,3) and (7, 9)?

$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $

---

Using $$ \red{ (10,3)}$$ as $$x_1, y_1$$

$ \frac{9- \red 3}{7- \red{10}} \\ = \frac{6}{-3} \\ = \boxed {-2 } $

Using $$ \red{ (7,9)} $$ as $$x_1, y_1$$

$ \frac{3- \red 9}{10- \red 7} \\ =\frac{-6}{3} \\ = \boxed{-2 } $

Problem 2

A line passes through (4, -2) and (4, 3). What is its slope?

$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $

---

---

Using $$ \red{ ( 4,3 )}$$ as $$x_1, y_1$$

$ = \frac{-2 - \red 3}{4- \red 4} \\ = \frac{-5}{ \color{red}{0}} \\ = \text{undefined} $

Using $$ \red{ ( 4, -2 )}$$ as $$x_1, y_1$$

$ = \frac{3- \red{-2}}{4- \red 4} \\ = \frac{5}{ \color{red}{0}} \\ = \text{undefined} $

Whenever the run of a line is zero, the slope is undefined. This is because there is a zero in the denominator of the slope! Any the slope of any vertical line is undefined .

Problem 3

A line passes through (2, 10) and (8, 7). What is its slope?

$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $

---

Using $$ \red{ ( 8, 7 )}$$ as $$x_1, y_1$$

$ \frac{10 - \red 7}{2 - \red 8} \\ = \frac{3}{-6} \\ = -\frac{1}{2} $

Using $$ \red{ ( 2,10 )}$$ as $$x_1, y_1$$

$ \frac{7 - \red {10}}{8- \red 2} \\ = \frac{-3}{6} \\ = -\frac{1}{2} $

Problem 4

A line passes through (7, 3) and (8, 5). What is its slope?

$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $

---

Using $$ \red{ (7,3 )}$$ as $$x_1, y_1$$

$$ \frac{ 5- \red 3}{8- \red 7} \\ = \frac{2}{1} \\ = 2 $$

Using $$ \red{ ( 8,5 )}$$ as $$x_1, y_1$$

$$ \frac{ 3- \red 5}{7- \red 8} \\= \frac{-2}{-1} \\ = 2 $$

Problem 5

A line passes through (12, 11) and (9, 5) . What is its slope?

$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $

---

Using $$ \red{ ( 5, 9)}$$ as $$x_1, y_1$$

$$ \frac{ 11 - \red 5}{12- \red 9} \\ = \frac{6}{3} \\ =2 $$

Using $$ \red{ (12, 11 )}$$ as $$x_1, y_1$$

$$ \frac{ 5- \red{ 11} }{9- \red { 12}} \\ = \frac{-6}{-3} \\ = 2 $$

Problem 6

What is the slope of a line that goes through (4, 2) and (4, 5)?

$ \frac{rise}{run}= \frac{y_{2}-y_{1}}{x_{2}-x_{1}} $

---

Using $$ \red{ ( 4,5 )}$$ as $$x_1, y_1$$

$$ \frac{ 2 - \red 5}{4- \red 4} \\ = \frac{ -3}{\color{red}{0}} \\ = undefined $$

Using $$ \red{ ( 4,2 )}$$ as $$x_1, y_1$$

$$ \frac{ 5 - \red 2}{4- \red 4} \\ = \frac{ 3}{\color{red}{0}} \\ = undefined $$

WARNING! Can you catch the error in the following problem Jennifer was trying to find the slope that goes through the points $$(\color{blue}{1},\color{red}{3})$$ and $$ (\color{blue}{2}, \color{red}{6})$$ . She was having a bit of trouble applying the slope formula, tried to calculate slope 3 times, and she came up with 3 different answers. Can you determine the correct answer?

Challenge Problem

Find the slope of A line Given Two Points.

Attempt #1

$ slope= \frac{rise}{run} \\= \frac{\color{red}{y_{2}-y_{1}}}{\color{blue}{x_{2}-x_{1}}} \\= \frac{6-3}{1-2} \\= \frac{3}{-1} =\boxed{-3} $

---

Attempt #2

$$ slope= \frac{rise}{run} \\= \frac{\color{red}{y_{2}-y_{1}}}{\color{blue}{x_{2}-x_{1}}} \\= \frac{6-3}{2-1} \\= \frac{3}{1} \\ = \boxed{3} $$

---

Attempt #3

$$ slope = \frac{rise}{run} \\= \frac{\color{red}{y_{2}-y_{1}}}{\color{blue}{x_{2}-x_{1}}} \\ =\frac{2-1}{6-3} \\ =\boxed{ \frac{1}{3}} $$

The correct answer is attempt #2.

In attempt #1, she did not consistently use the points. What she did, in attempt one, was :

$$ \frac{\color{red}{y{\boxed{_2}}-y_{1}}}{\color{blue}{x\boxed{_{1}}-x_{2}}} $$

The problem with attempt #3 was reversing the rise and run. She put the x values in the numerator( top) and the y values in the denominator which, of course, is the opposite!

$$ \cancel {\frac{\color{blue}{x_{2}-x_{1}}}{\color{red}{y_{2}-y_{1}}}} $$

Slope Practice Problem Generator

You can practice solving this sort of problem as much as you would like with the slope problem generator below.

It will randomly generate numbers and ask for the slope of the line through those two points. You can chose how large the numbers will be by adjusting the difficulty level.

The Thigh High Socks With the 3 Lines and Trasparent Sections Between the Lines

Source: https://www.mathwarehouse.com/algebra/linear_equation/slope-of-a-line.php

Share this post