A Family of Pdfs That Has Been Used to Approximate the Distribution of Income

Probability distribution

Pareto Type I

Probability density role Pareto Type I probability density functions for various ${\displaystyle \alpha }$ with ${\displaystyle x_{\mathrm {m} }=1.}$ As ${\displaystyle \blastoff \rightarrow \infty ,}$ the distribution approaches ${\displaystyle \delta (x-x_{\mathrm {m} }),}$ where ${\displaystyle \delta }$ is the Dirac delta function.
Cumulative distribution function Pareto Type I cumulative distribution functions for diverse ${\displaystyle \alpha }$ with ${\displaystyle x_{\mathrm {m} }=i.}$
Parameters	${\displaystyle x_{\mathrm {g} }>0}$ scale (real) ${\displaystyle \blastoff >0}$ shape (real)
Support	${\displaystyle x\in [x_{\mathrm {m} },\infty )}$
PDF	${\displaystyle {\frac {\blastoff x_{\mathrm {yard} }^{\alpha }}{x^{\blastoff +ane}}}}$
CDF	${\displaystyle 1-\left({\frac {x_{\mathrm {thou} }}{x}}\right)^{\blastoff }}$
Quantile	${\displaystyle x_{\mathrm {g} }{(1-p)}^{-{\frac {1}{\alpha }}}}$
Hateful	${\displaystyle {\begin{cases}\infty &{\text{for }}\blastoff \leq ane\\{\dfrac {\alpha x_{\mathrm {m} }}{\alpha -1}}&{\text{for }}\alpha >1\finish{cases}}}$
Median	${\displaystyle x_{\mathrm {chiliad} }{\sqrt[{\alpha }]{two}}}$
Style	${\displaystyle x_{\mathrm {k} }}$
Variance	${\displaystyle {\begin{cases}\infty &{\text{for }}\alpha \leq two\\{\dfrac {x_{\mathrm {thou} }^{ii}\alpha }{(\blastoff -one)^{2}(\alpha -2)}}&{\text{for }}\alpha >2\stop{cases}}}$
Skewness	${\displaystyle {\frac {2(1+\blastoff )}{\alpha -three}}{\sqrt {\frac {\alpha -two}{\alpha }}}{\text{ for }}\alpha >three}$
Ex. kurtosis	${\displaystyle {\frac {6(\blastoff ^{three}+\alpha ^{2}-6\alpha -2)}{\blastoff (\blastoff -3)(\alpha -4)}}{\text{ for }}\alpha >four}$
Entropy	${\displaystyle \log \left(\left({\frac {x_{\mathrm {m} }}{\alpha }}\right)\,e^{i+{\tfrac {ane}{\blastoff }}}\correct)}$
MGF	does non be
CF	${\displaystyle \alpha (-ix_{\mathrm {k} }t)^{\alpha }\Gamma (-\alpha ,-ix_{\mathrm {thousand} }t)}$
Fisher information	${\displaystyle {\mathcal {I}}(x_{\mathrm {chiliad} },\alpha )={\brainstorm{bmatrix}{\dfrac {\alpha }{x_{\mathrm {thousand} }^{2}}}&-{\dfrac {i}{x_{\mathrm {1000} }}}\\-{\dfrac {one}{x_{\mathrm {m} }}}&{\dfrac {ane}{\alpha ^{two}}}\end{bmatrix}}}$ Correct: ${\displaystyle {\mathcal {I}}(x_{\mathrm {m} },\alpha )={\begin{bmatrix}{\dfrac {\alpha ^{2}}{x_{\mathrm {m} }^{2}}}&0\\0&{\dfrac {one}{\blastoff ^{two}}}\end{bmatrix}}}$

The Pareto distribution, named after the Italian civil engineer, economist, and sociologist Vilfredo Pareto,^[ane] ( Italian: [] pə-RAY-toh),^[2] is a power-law probability distribution that is used in description of social, quality command, scientific, geophysical, actuarial, and many other types of observable phenomena. Originally practical to describing the distribution of wealth in a order, fitting the trend that a large portion of wealth is held past a pocket-sized fraction of the population.^{[three] [iv]} The Pareto principle or "eighty-20 rule" stating that lxxx% of outcomes are due to 20% of causes was named in honour of Pareto, merely the concepts are distinct, and just Pareto distributions with shape value ( α ) of log_four5 ≈ 1.16 precisely reverberate it. Empirical observation has shown that this lxxx-twenty distribution fits a wide range of cases, including natural phenomena^[v] and man activities.^{[vi] [7]}

Definitions [edit]

If X is a random variable with a Pareto (Blazon I) distribution,^[viii] and so the probability that X is greater than some number x, i.e. the survival office (likewise called tail function), is given by

${\displaystyle {\overline {F}}(x)=\Pr(X>10)={\brainstorm{cases}\left({\frac {x_{\mathrm {m} }}{10}}\right)^{\alpha }&x\geq x_{\mathrm {m} },\\1&x<x_{\mathrm {yard} },\end{cases}}}$

where x ₁₀₀₀ is the (necessarily positive) minimum possible value of X, and α is a positive parameter. The Pareto Type I distribution is characterized past a calibration parameter x _thou and a shape parameter α, which is known as the tail alphabetize. When this distribution is used to model the distribution of wealth, then the parameter α is called the Pareto index.

Cumulative distribution function [edit]

From the definition, the cumulative distribution part of a Pareto random variable with parameters α and x _yard is

${\displaystyle F_{10}(x)={\begin{cases}1-\left({\frac {x_{\mathrm {1000} }}{ten}}\right)^{\alpha }&x\geq x_{\mathrm {k} },\\0&10<x_{\mathrm {m} }.\end{cases}}}$

Probability density role [edit]

It follows (by differentiation) that the probability density function is

${\displaystyle f_{X}(ten)={\begin{cases}{\frac {\blastoff x_{\mathrm {m} }^{\alpha }}{ten^{\alpha +one}}}&ten\geq x_{\mathrm {m} },\\0&x<x_{\mathrm {m} }.\stop{cases}}}$

When plotted on linear axes, the distribution assumes the familiar J-shaped bend which approaches each of the orthogonal axes asymptotically. All segments of the curve are self-similar (subject to appropriate scaling factors). When plotted in a log-log plot, the distribution is represented by a straight line.

Properties [edit]

Moments and characteristic function [edit]

• The expected value of a random variable following a Pareto distribution is

${\displaystyle \operatorname {E} (10)={\begin{cases}\infty &\blastoff \leq ane,\\{\frac {\blastoff x_{\mathrm {m} }}{\blastoff -one}}&\blastoff >1.\finish{cases}}}$

• The variance of a random variable following a Pareto distribution is

${\displaystyle \operatorname {Var} (X)={\begin{cases}\infty &\alpha \in (i,two],\\\left({\frac {x_{\mathrm {1000} }}{\alpha -one}}\correct)^{two}{\frac {\blastoff }{\alpha -2}}&\blastoff >2.\stop{cases}}}$

(If α ≤ ane, the variance does not be.)

• The raw moments are

${\displaystyle \mu _{n}'={\begin{cases}\infty &\alpha \leq due north,\\{\frac {\blastoff x_{\mathrm {m} }^{north}}{\alpha -due north}}&\alpha >n.\terminate{cases}}}$

• The moment generating part is only defined for not-positive values t ≤ 0 as

${\displaystyle One thousand\left(t;\blastoff ,x_{\mathrm {m} }\right)=\operatorname {E} \left[e^{tX}\right]=\blastoff (-x_{\mathrm {m} }t)^{\blastoff }\Gamma (-\alpha ,-x_{\mathrm {thou} }t)}$

${\displaystyle Grand\left(0,\alpha ,x_{\mathrm {thousand} }\right)=1.}$

Thus, since the expectation does not converge on an open interval containing ${\displaystyle t=0}$ we say that the moment generating function does not be.

• The characteristic function is given by

${\displaystyle \varphi (t;\alpha ,x_{\mathrm {yard} })=\alpha (-ix_{\mathrm {k} }t)^{\alpha }\Gamma (-\alpha ,-ix_{\mathrm {m} }t),}$

where Γ(a,x) is the incomplete gamma office.

The parameters may exist solved for using the method of moments.^[ix]

Provisional distributions [edit]

The conditional probability distribution of a Pareto-distributed random variable, given the issue that information technology is greater than or equal to a detail number ${\displaystyle x_{1}}$ exceeding ${\displaystyle x_{\text{m}}}$ , is a Pareto distribution with the aforementioned Pareto index ${\displaystyle \alpha }$ but with minimum ${\displaystyle x_{i}}$ instead of ${\displaystyle x_{\text{one thousand}}}$ . This implies that the conditional expected value (if it is finite, i.e. ${\displaystyle \blastoff >1}$ ) is proportional to ${\displaystyle x_{i}}$ . In case of random variables that describe the lifetime of an object, this means that life expectancy is proportional to age, and is called the Lindy issue or Lindy's Law.^[10]

A characterization theorem [edit]

Suppose ${\displaystyle X_{one},X_{two},X_{3},\dotsc }$ are independent identically distributed random variables whose probability distribution is supported on the interval ${\displaystyle [x_{\text{m}},\infty )}$ for some ${\displaystyle x_{\text{chiliad}}>0}$ . Suppose that for all ${\displaystyle n}$ , the two random variables ${\displaystyle \min\{X_{1},\dotsc ,X_{n}\}}$ and ${\displaystyle (X_{1}+\dotsb +X_{northward})/\min\{X_{1},\dotsc ,X_{due north}\}}$ are independent. Then the common distribution is a Pareto distribution.^{[ citation needed ]}

Geometric mean [edit]

The geometric mean (G) is^[11]

${\displaystyle Grand=x_{\text{one thousand}}\exp \left({\frac {i}{\alpha }}\correct).}$

Harmonic mean [edit]

The harmonic hateful (H) is^[11]

${\displaystyle H=x_{\text{grand}}\left(1+{\frac {i}{\blastoff }}\right).}$

Graphical representation [edit]

The characteristic curved 'long tail' distribution when plotted on a linear scale, masks the underlying simplicity of the function when plotted on a log-log graph, which and then takes the form of a straight line with negative gradient: It follows from the formula for the probability density function that for 10 ≥ x _thousand,

${\displaystyle \log f_{X}(ten)=\log \left(\alpha {\frac {x_{\mathrm {g} }^{\alpha }}{x^{\blastoff +1}}}\correct)=\log(\alpha x_{\mathrm {chiliad} }^{\alpha })-(\alpha +ane)\log ten.}$

Since α is positive, the slope −(α + 1) is negative.

[edit]

Generalized Pareto distributions [edit]

There is a hierarchy ^{[eight] [12]} of Pareto distributions known as Pareto Blazon I, Two, III, IV, and Feller–Pareto distributions.^{[8] [12] [thirteen]} Pareto Blazon Iv contains Pareto Type I–Three as special cases. The Feller–Pareto^{[12] [xiv]} distribution generalizes Pareto Type 4.

Pareto types I–4 [edit]

The Pareto distribution hierarchy is summarized in the next table comparing the survival functions (complementary CDF).

When μ = 0, the Pareto distribution Type Ii is also known equally the Lomax distribution.^[15]

In this department, the symbol 10 _thou, used before to indicate the minimum value of x, is replaced byσ.

Pareto distributions

	${\displaystyle {\overline {F}}(x)=ane-F(10)}$	Back up	Parameters
Type I	${\displaystyle \left[{\frac {x}{\sigma }}\right]^{-\blastoff }}$	${\displaystyle ten\geq \sigma }$	${\displaystyle \sigma >0,\alpha }$
Type Ii	${\displaystyle \left[1+{\frac {x-\mu }{\sigma }}\correct]^{-\alpha }}$	${\displaystyle x\geq \mu }$	${\displaystyle \mu \in \mathbb {R} ,\sigma >0,\alpha }$
Lomax	${\displaystyle \left[1+{\frac {x}{\sigma }}\right]^{-\alpha }}$	${\displaystyle x\geq 0}$	${\displaystyle \sigma >0,\alpha }$
Blazon III	${\displaystyle \left[ane+\left({\frac {10-\mu }{\sigma }}\right)^{1/\gamma }\correct]^{-1}}$	${\displaystyle x\geq \mu }$	${\displaystyle \mu \in \mathbb {R} ,\sigma ,\gamma >0}$
Type IV	${\displaystyle \left[one+\left({\frac {x-\mu }{\sigma }}\correct)^{i/\gamma }\correct]^{-\blastoff }}$	${\displaystyle x\geq \mu }$	${\displaystyle \mu \in \mathbb {R} ,\sigma ,\gamma >0,\blastoff }$

The shape parameter α is the tail index, μ is location, σ is calibration, γ is an inequality parameter. Some special cases of Pareto Type (IV) are

${\displaystyle P(IV)(\sigma ,\sigma ,one,\alpha )=P(I)(\sigma ,\alpha ),}$

${\displaystyle P(Four)(\mu ,\sigma ,1,\alpha )=P(2)(\mu ,\sigma ,\blastoff ),}$

${\displaystyle P(IV)(\mu ,\sigma ,\gamma ,1)=P(III)(\mu ,\sigma ,\gamma ).}$

The finiteness of the hateful, and the existence and the finiteness of the variance depend on the tail index α (inequality alphabetize γ). In particular, partial δ-moments are finite for some δ > 0, as shown in the table below, where δ is not necessarily an integer.

Moments of Pareto I–Four distributions (instance μ = 0)

	${\displaystyle \operatorname {E} [Ten]}$	Condition	${\displaystyle \operatorname {E} [X^{\delta }]}$	Condition
Blazon I	${\displaystyle {\frac {\sigma \alpha }{\alpha -1}}}$	${\displaystyle \alpha >1}$	${\displaystyle {\frac {\sigma ^{\delta }\alpha }{\alpha -\delta }}}$	${\displaystyle \delta <\alpha }$
Type Ii	${\displaystyle {\frac {\sigma }{\alpha -one}}+\mu }$	${\displaystyle \alpha >one}$	${\displaystyle {\frac {\sigma ^{\delta }\Gamma (\alpha -\delta )\Gamma (1+\delta )}{\Gamma (\alpha )}}}$	${\displaystyle 0<\delta <\alpha }$
Type Iii	${\displaystyle \sigma \Gamma (1-\gamma )\Gamma (1+\gamma )}$	${\displaystyle -ane<\gamma <1}$	${\displaystyle \sigma ^{\delta }\Gamma (1-\gamma \delta )\Gamma (ane+\gamma \delta )}$	${\displaystyle -\gamma ^{-1}<\delta <\gamma ^{-1}}$
Blazon IV	${\displaystyle {\frac {\sigma \Gamma (\alpha -\gamma )\Gamma (1+\gamma )}{\Gamma (\alpha )}}}$	${\displaystyle -one<\gamma <\alpha }$	${\displaystyle {\frac {\sigma ^{\delta }\Gamma (\alpha -\gamma \delta )\Gamma (1+\gamma \delta )}{\Gamma (\blastoff )}}}$	${\displaystyle -\gamma ^{-1}<\delta <\blastoff /\gamma }$

Feller–Pareto distribution [edit]

Feller^{[12] [14]} defines a Pareto variable by transformation U =Y ⁻¹ − one of a beta random variable Y, whose probability density function is

${\displaystyle f(y)={\frac {y^{\gamma _{1}-1}(1-y)^{\gamma _{2}-1}}{B(\gamma _{1},\gamma _{2})}},\qquad 0<y<1;\gamma _{1},\gamma _{2}>0,}$

where B( ) is the beta part. If

${\displaystyle W=\mu +\sigma (Y^{-i}-1)^{\gamma },\qquad \sigma >0,\gamma >0,}$

then W has a Feller–Pareto distribution FP(μ, σ, γ, γ ₁, γ ₂).^[8]

If ${\displaystyle U_{1}\sim \Gamma (\delta _{i},1)}$ and ${\displaystyle U_{2}\sim \Gamma (\delta _{2},1)}$ are independent Gamma variables, another construction of a Feller–Pareto (FP) variable is^[xvi]

${\displaystyle W=\mu +\sigma \left({\frac {U_{1}}{U_{2}}}\correct)^{\gamma }}$

and nosotros write W ~ FP(μ, σ, γ, δ _ane, δ ₂). Special cases of the Feller–Pareto distribution are

${\displaystyle FP(\sigma ,\sigma ,i,1,\alpha )=P(I)(\sigma ,\alpha )}$

${\displaystyle FP(\mu ,\sigma ,1,ane,\alpha )=P(II)(\mu ,\sigma ,\blastoff )}$

${\displaystyle FP(\mu ,\sigma ,\gamma ,1,ane)=P(III)(\mu ,\sigma ,\gamma )}$

${\displaystyle FP(\mu ,\sigma ,\gamma ,ane,\alpha )=P(Iv)(\mu ,\sigma ,\gamma ,\alpha ).}$

Relation to the exponential distribution [edit]

The Pareto distribution is related to the exponential distribution as follows. If Ten is Pareto-distributed with minimum x _thousand and alphabetizeα, then

${\displaystyle Y=\log \left({\frac {X}{x_{\mathrm {m} }}}\right)}$

is exponentially distributed with rate parameterα. Equivalently, if Y is exponentially distributed with rateα, then

${\displaystyle x_{\mathrm {thou} }e^{Y}}$

is Pareto-distributed with minimum 10 _m and indexα.

This can be shown using the standard change-of-variable techniques:

${\displaystyle {\begin{aligned}\Pr(Y<y)&=\Pr \left(\log \left({\frac {X}{x_{\mathrm {thou} }}}\right)<y\right)\\&=\Pr(X<x_{\mathrm {m} }e^{y})=1-\left({\frac {x_{\mathrm {1000} }}{x_{\mathrm {m} }due east^{y}}}\right)^{\alpha }=1-due east^{-\alpha y}.\end{aligned}}}$

The last expression is the cumulative distribution function of an exponential distribution with rateα.

Pareto distribution tin exist constructed by hierarchical exponential distributions.^[17] Let ${\displaystyle \phi |a\sim {\text{Exp}}(a)}$ and ${\displaystyle \eta |\phi \sim {\text{Exp}}(\phi )}$ . And then we accept ${\displaystyle p(\eta |a)={\frac {a}{(a+\eta )^{2}}}}$ and, as a result, ${\displaystyle a+\eta \sim {\text{Pareto}}(a,1)}$ .

More than in full general, if ${\displaystyle \lambda \sim {\text{Gamma}}(\alpha ,\beta )}$ (shape-charge per unit parametrization) and ${\displaystyle \eta |\lambda \sim {\text{Exp}}(\lambda )}$ , then ${\displaystyle \beta +\eta \sim {\text{Pareto}}(\beta ,\alpha )}$ .

Equivalently, if ${\displaystyle Y\sim {\text{Gamma}}(\alpha ,1)}$ and ${\displaystyle X\sim {\text{Exp}}(1)}$ , and so ${\displaystyle x_{\text{m}}\!\left(i+{\frac {10}{Y}}\right)\sim {\text{Pareto}}(x_{\text{m}},\blastoff )}$ .

Relation to the log-normal distribution [edit]

The Pareto distribution and log-normal distribution are alternative distributions for describing the same types of quantities. I of the connections betwixt the two is that they are both the distributions of the exponential of random variables distributed according to other common distributions, respectively the exponential distribution and normal distribution. (Run into the previous section.)

Relation to the generalized Pareto distribution [edit]

The Pareto distribution is a special example of the generalized Pareto distribution, which is a family of distributions of similar form, just containing an extra parameter in such a style that the back up of the distribution is either bounded below (at a variable point), or bounded both above and below (where both are variable), with the Lomax distribution as a special instance. This family too contains both the unshifted and shifted exponential distributions.

The Pareto distribution with scale ${\displaystyle x_{k}}$ and shape ${\displaystyle \alpha }$ is equivalent to the generalized Pareto distribution with location ${\displaystyle \mu =x_{m}}$ , calibration ${\displaystyle \sigma =x_{m}/\blastoff }$ and shape ${\displaystyle \xi =one/\blastoff }$ . Vice versa ane can get the Pareto distribution from the GPD past ${\displaystyle x_{chiliad}=\sigma /\eleven }$ and ${\displaystyle \alpha =1/\11 }$ .

Divisional Pareto distribution [edit]

Bounded Pareto

Parameters	${\displaystyle L>0}$ location (existent) ${\displaystyle H>L}$ location (existent) ${\displaystyle \alpha >0}$ shape (real)
Support	${\displaystyle Fifty\leqslant x\leqslant H}$
PDF	${\displaystyle {\frac {\blastoff Fifty^{\alpha }x^{-\alpha -1}}{1-\left({\frac {Fifty}{H}}\correct)^{\alpha }}}}$
CDF	${\displaystyle {\frac {1-L^{\alpha }x^{-\blastoff }}{one-\left({\frac {L}{H}}\right)^{\alpha }}}}$
Mean	${\displaystyle {\frac {Fifty^{\alpha }}{1-\left({\frac {L}{H}}\correct)^{\alpha }}}\cdot \left({\frac {\alpha }{\blastoff -1}}\right)\cdot \left({\frac {1}{L^{\alpha -ane}}}-{\frac {1}{H^{\alpha -1}}}\right),\blastoff \neq 1}$ ${\displaystyle {\frac {{H}{50}}{{H}-{L}}}\ln {\frac {H}{Fifty}},\alpha =1}$
Median	${\displaystyle L\left(ane-{\frac {1}{ii}}\left(1-\left({\frac {L}{H}}\right)^{\alpha }\right)\right)^{-{\frac {1}{\alpha }}}}$
Variance	${\displaystyle {\frac {Fifty^{\alpha }}{1-\left({\frac {L}{H}}\right)^{\alpha }}}\cdot \left({\frac {\alpha }{\alpha -2}}\right)\cdot \left({\frac {1}{50^{\alpha -2}}}-{\frac {i}{H^{\alpha -two}}}\right),\alpha \neq 2}$ ${\displaystyle {\frac {2{H}^{2}{50}^{2}}{{H}^{2}-{50}^{two}}}\ln {\frac {H}{L}},\alpha =2}$ (this is the second raw moment, not the variance)
Skewness	${\displaystyle {\frac {L^{\alpha }}{1-\left({\frac {L}{H}}\right)^{\alpha }}}\cdot {\frac {\blastoff *(L^{k-\blastoff }-H^{k-\alpha })}{(\blastoff -k)}},\alpha \neq j}$ (this is the kth raw moment, not the skewness)

The bounded (or truncated) Pareto distribution has three parameters: α, L and H. As in the standard Pareto distribution α determines the shape. Fifty denotes the minimal value, and H denotes the maximal value.

The probability density role is

${\displaystyle {\frac {\alpha L^{\alpha }10^{-\alpha -one}}{1-\left({\frac {L}{H}}\right)^{\blastoff }}}}$ ,

where L ≤10 ≤H, and α > 0.

Generating bounded Pareto random variables [edit]

If U is uniformly distributed on (0, one), then applying changed-transform method ^[xviii]

${\displaystyle U={\frac {ane-Fifty^{\alpha }x^{-\alpha }}{1-({\frac {L}{H}})^{\alpha }}}}$

${\displaystyle x=\left(-{\frac {UH^{\alpha }-UL^{\blastoff }-H^{\blastoff }}{H^{\alpha }Fifty^{\blastoff }}}\correct)^{-{\frac {1}{\alpha }}}}$

is a divisional Pareto-distributed.

Symmetric Pareto distribution [edit]

The purpose of Symmetric Pareto distribution and Nothing Symmetric Pareto distribution is to capture some special statistical distribution with a sharp probability top and symmetric long probability tails. These two distributions are derived from Pareto distribution. Long probability tail normally means that probability decays slowly. Pareto distribution performs plumbing equipment task in many cases. But if the distribution has symmetric structure with two slow decaying tails, Pareto could not do it. And so Symmetric Pareto or Zero Symmetric Pareto distribution is applied instead.^[nineteen]

The Cumulative distribution function (CDF) of Symmetric Pareto distribution is divers as post-obit:^[xix]

${\displaystyle F(X)=P(x<Ten)={\begin{cases}{\tfrac {ane}{2}}({b \over 2b-X})^{a}&X<b\\1-{\tfrac {1}{2}}({\tfrac {b}{X}})^{a}&X\geq b\end{cases}}}$

The corresponding probability density function (PDF) is:^[xix]

${\displaystyle p(ten)={ab^{a} \over 2(b+\left\vert x-b\correct\vert )^{a+i}},X\in R}$

This distribution has two parameters: a and b. Information technology is symmetric past b. Then the mathematic expectation is b. When, it has variance as following:

${\displaystyle E((x-b)^{2})=\int _{-\infty }^{\infty }(x-b)^{two}p(x)dx={2b^{2} \over (a-two)(a-1)}}$

The CDF of Zero Symmetric Pareto (ZSP) distribution is divers equally following:

${\displaystyle F(10)=P(10<10)={\begin{cases}{\tfrac {i}{2}}({b \over b-10})^{a}&X<0\\ane-{\tfrac {one}{2}}({\tfrac {b}{b+X}})^{a}&X\geq 0\stop{cases}}}$

The respective PDF is:

${\displaystyle p(x)={ab^{a} \over ii(b+\left\vert x\right\vert )^{a+ane}},X\in R}$

This distribution is symmetric by zero. Parameter a is related to the decay rate of probability and (a/2b) represents summit magnitude of probability.^[19]

Multivariate Pareto distribution [edit]

The univariate Pareto distribution has been extended to a multivariate Pareto distribution.^[20]

Statistical inference [edit]

Estimation of parameters [edit]

The likelihood function for the Pareto distribution parameters α and ten _g, given an contained sample x = (x _ane,x ₂, ...,x_northward ), is

${\displaystyle L(\alpha ,x_{\mathrm {m} })=\prod _{i=1}^{northward}\alpha {\frac {x_{\mathrm {k} }^{\blastoff }}{x_{i}^{\alpha +i}}}=\alpha ^{n}x_{\mathrm {thousand} }^{northward\alpha }\prod _{i=one}^{n}{\frac {one}{x_{i}^{\blastoff +ane}}}.}$

Therefore, the logarithmic likelihood function is

${\displaystyle \ell (\alpha ,x_{\mathrm {one thousand} })=north\ln \alpha +n\alpha \ln x_{\mathrm {m} }-(\alpha +one)\sum _{i=1}^{n}\ln x_{i}.}$

It tin can exist seen that ${\displaystyle \ell (\blastoff ,x_{\mathrm {m} })}$ is monotonically increasing with x _thou, that is, the greater the value of ten _grand, the greater the value of the likelihood office. Hence, since ten ≥ x _{one thousand}, we conclude that

${\displaystyle {\widehat {x}}_{\mathrm {m} }=\min _{i}{x_{i}}.}$

To find the calculator for α, nosotros compute the corresponding fractional derivative and decide where it is nix:

${\displaystyle {\frac {\partial \ell }{\partial \alpha }}={\frac {due north}{\blastoff }}+due north\ln x_{\mathrm {m} }-\sum _{i=1}^{north}\ln x_{i}=0.}$

Thus the maximum likelihood estimator for α is:

${\displaystyle {\widehat {\alpha }}={\frac {n}{\sum _{i}\ln(x_{i}/{\widehat {x}}_{\mathrm {m} })}}.}$

The expected statistical error is:^[21]

${\displaystyle \sigma ={\frac {\widehat {\alpha }}{\sqrt {n}}}.}$

Malik (1970)^[22] gives the exact joint distribution of ${\displaystyle ({\hat {x}}_{\mathrm {one thousand} },{\lid {\alpha }})}$ . In item, ${\displaystyle {\hat {x}}_{\mathrm {m} }}$ and ${\displaystyle {\hat {\alpha }}}$ are independent and ${\displaystyle {\chapeau {ten}}_{\mathrm {m} }}$ is Pareto with scale parameter x _m and shape parameter nα, whereas ${\displaystyle {\hat {\blastoff }}}$ has an inverse-gamma distribution with shape and scale parameters north − one and nα, respectively.

Occurrence and applications [edit]

General [edit]

Vilfredo Pareto originally used this distribution to describe the resource allotment of wealth amid individuals since it seemed to show rather well the mode that a larger portion of the wealth of whatever club is owned by a smaller percentage of the people in that club. He also used it to draw distribution of income.^[4] This idea is sometimes expressed more simply as the Pareto principle or the "eighty-20 rule" which says that twenty% of the population controls fourscore% of the wealth.^[23] However, the 80-20 rule corresponds to a item value of α, and in fact, Pareto's data on British income taxes in his Cours d'économie politique indicates that about 30% of the population had about 70% of the income.^{[ citation needed ]} The probability density office (PDF) graph at the get-go of this commodity shows that the "probability" or fraction of the population that owns a small amount of wealth per person is rather high, and then decreases steadily as wealth increases. (The Pareto distribution is not realistic for wealth for the lower end, however. In fact, net worth may fifty-fifty be negative.) This distribution is non limited to describing wealth or income, but to many situations in which an equilibrium is establish in the distribution of the "small" to the "large". The following examples are sometimes seen as approximately Pareto-distributed:

• The sizes of man settlements (few cities, many hamlets/villages)^{[24] [25]}
• File size distribution of Net traffic which uses the TCP protocol (many smaller files, few larger ones)^[24]
• Hard disk error rates^[26]
• Clusters of Bose–Einstein condensate near absolute zero^[27]

• The values of oil reserves in oil fields (a few big fields, many small fields)^[24]
• The length distribution in jobs assigned to supercomputers (a few large ones, many small ones)^[28]
• The standardized toll returns on individual stocks ^[24]
• Sizes of sand particles ^[24]
• The size of meteorites
• Severity of big prey losses for sure lines of business organisation such every bit full general liability, commercial auto, and workers compensation.^{[29] [30]}
• Amount of time a user on Steam volition spend playing unlike games. (Some games get played a lot, but nearly become played almost never.) [2]^{[ original enquiry? ]}
• In hydrology the Pareto distribution is applied to extreme events such every bit annually maximum ane-day rainfalls and river discharges.^[31] The blue picture illustrates an example of plumbing fixtures the Pareto distribution to ranked annually maximum one-twenty-four hours rainfalls showing as well the ninety% confidence belt based on the binomial distribution. The rainfall information are represented by plotting positions as part of the cumulative frequency analysis.
• In Electric Utility Distribution Reliability (80% of the Customer Minutes Interrupted occur on approximately twenty% of the days in a given year).

Relation to Zipf'south law [edit]

The Pareto distribution is a continuous probability distribution. Zipf's police force, also sometimes called the zeta distribution, is a discrete distribution, separating the values into a unproblematic ranking. Both are a simple power law with a negative exponent, scaled so that their cumulative distributions equal one. Zipf'due south can exist derived from the Pareto distribution if the ${\displaystyle x}$ values (incomes) are binned into ${\displaystyle Due north}$ ranks so that the number of people in each bin follows a 1/rank pattern. The distribution is normalized by defining ${\displaystyle x_{m}}$ so that ${\displaystyle \alpha x_{\mathrm {m} }^{\blastoff }={\frac {1}{H(N,\alpha -1)}}}$ where ${\displaystyle H(Due north,\blastoff -one)}$ is the generalized harmonic number. This makes Zipf'south probability density function derivable from Pareto'due south.

${\displaystyle f(x)={\frac {\alpha x_{\mathrm {m} }^{\alpha }}{x^{\alpha +one}}}={\frac {1}{x^{southward}H(N,s)}}}$

where ${\displaystyle due south=\alpha -1}$ and ${\displaystyle ten}$ is an integer representing rank from ane to North where North is the highest income bracket. So a randomly selected person (or word, website link, or city) from a population (or linguistic communication, internet, or country) has ${\displaystyle f(x)}$ probability of ranking ${\displaystyle x}$ .

Relation to the "Pareto principle" [edit]

The "lxxx–xx police", according to which twenty% of all people receive 80% of all income, and 20% of the most flush twenty% receive 80% of that 80%, and and so on, holds precisely when the Pareto alphabetize is ${\displaystyle \alpha =\log _{4}five={\cfrac {\log _{10}5}{\log _{10}4}}\approx ane.161}$ . This result tin can exist derived from the Lorenz curve formula given below. Moreover, the following have been shown^[32] to be mathematically equivalent:

• Income is distributed co-ordinate to a Pareto distribution with index α > 1.
• In that location is some number 0 ≤p ≤ 1/2 such that 100p % of all people receive 100(1 −p)% of all income, and similarly for every real (non necessarily integer) n > 0, 100p^northward  % of all people receive 100(1 −p) ⁿ percentage of all income. α and p are related by

${\displaystyle 1-{\frac {1}{\alpha }}={\frac {\ln(i-p)}{\ln(p)}}={\frac {\ln((1-p)^{n})}{\ln(p^{due north})}}}$

This does non apply only to income, just as well to wealth, or to anything else that can be modeled by this distribution.

This excludes Pareto distributions in which 0 <α ≤ i, which, as noted higher up, have an infinite expected value, and and then cannot reasonably model income distribution.

Relation to Cost's law [edit]

Price'due south square root law is sometimes offered every bit a property of or as similar to the Pareto distribution. However, the police only holds in the case that ${\displaystyle \alpha =1}$ . Note that in this case, the total and expected corporeality of wealth are not defined, and the rule just applies asymptotically to random samples. The extended Pareto Principle mentioned higher up is a far more general rule.

Lorenz curve and Gini coefficient [edit]

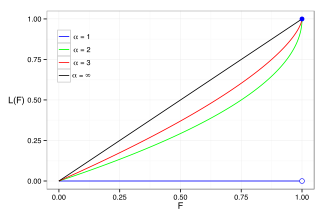
Lorenz curves for a number of Pareto distributions. The case α = ∞ corresponds to perfectly equal distribution (K = 0) and the α = 1 line corresponds to complete inequality (G = i)

The Lorenz bend is often used to characterize income and wealth distributions. For any distribution, the Lorenz curve L(F) is written in terms of the PDF f or the CDF F equally

${\displaystyle L(F)={\frac {\int _{x_{\mathrm {thou} }}^{x(F)}xf(x)\,dx}{\int _{x_{\mathrm {yard} }}^{\infty }xf(x)\,dx}}={\frac {\int _{0}^{F}x(F')\,dF'}{\int _{0}^{1}x(F')\,dF'}}}$

where x(F) is the changed of the CDF. For the Pareto distribution,

${\displaystyle x(F)={\frac {x_{\mathrm {chiliad} }}{(1-F)^{\frac {1}{\blastoff }}}}}$

and the Lorenz curve is calculated to be

${\displaystyle L(F)=ane-(1-F)^{one-{\frac {1}{\alpha }}},}$

For ${\displaystyle 0<\alpha \leq 1}$ the denominator is space, yielding L=0. Examples of the Lorenz bend for a number of Pareto distributions are shown in the graph on the right.

According to Oxfam (2016) the richest 62 people have as much wealth equally the poorest half of the world's population.^[33] Nosotros can estimate the Pareto alphabetize that would employ to this situation. Letting ε equal ${\displaystyle 62/(seven\times 10^{nine})}$ we accept:

${\displaystyle Fifty(1/2)=i-Fifty(one-\varepsilon )}$

or

${\displaystyle 1-(1/ii)^{1-{\frac {1}{\alpha }}}=\varepsilon ^{1-{\frac {one}{\alpha }}}}$

The solution is that α equals about 1.fifteen, and about 9% of the wealth is owned past each of the two groups. But actually the poorest 69% of the earth adult population owns only nigh 3% of the wealth.^[34]

The Gini coefficient is a measure of the deviation of the Lorenz curve from the equidistribution line which is a line connecting [0, 0] and [1, 1], which is shown in black (α = ∞) in the Lorenz plot on the correct. Specifically, the Gini coefficient is twice the area between the Lorenz curve and the equidistribution line. The Gini coefficient for the Pareto distribution is and then calculated (for ${\displaystyle \alpha \geq 1}$ ) to be

${\displaystyle G=1-two\left(\int _{0}^{1}L(F)\,dF\right)={\frac {1}{2\alpha -1}}}$

(see Aaberge 2005).

Computational methods [edit]

Random sample generation [edit]

Random samples tin can exist generated using inverse transform sampling. Given a random variate U drawn from the uniform distribution on the unit of measurement interval (0, 1], the variate T given by

${\displaystyle T={\frac {x_{\mathrm {thousand} }}{U^{1/\alpha }}}}$

is Pareto-distributed.^[35] If U is uniformly distributed on [0, 1), it tin can exist exchanged with (1 −U).

See also [edit]

• Bradford's law
• Gutenberg–Richter law
• Matthew result
• Pareto assay
• Pareto efficiency
• Pareto interpolation
• Power police force probability distributions
• Sturgeon'south law
• Traffic generation model
• Zipf'southward law
• Heavy-tailed distribution

References [edit]

1. ^ Amoroso, Luigi (1938). "VILFREDO PARETO". Econometrica (Pre-1986); Jan 1938; half dozen, one; ProQuest. 6.
2. ^ "Pareto". Merriam-Webster Dictionary . Retrieved 28 July 2019.
3. ^ Pareto, Vilfredo (1898). "Cours d'economie politique". Journal of Political Economy. half dozen. doi:10.1086/250536.
4. ^ ^{a b} Pareto, Vilfredo, Cours d'Économie Politique: Nouvelle édition par G.-H. Bousquet et G. Busino, Librairie Droz, Geneva, 1964, pp. 299–345. Original book archived
5. ^ VAN MONTFORT, Yard.A.J. (1986). "The Generalized Pareto distribution applied to rainfall depths". Hydrological Sciences Journal. 31 (2): 151–162. doi:10.1080/02626668609491037.
6. ^ Oancea, Bogdan (2017). "Income inequality in Romania: The exponential-Pareto distribution". Physica A: Statistical Mechanics and Its Applications. 469: 486–498. Bibcode:2017PhyA..469..486O. doi:ten.1016/j.physa.2016.11.094.
7. ^ Morella, Matteo. "Pareto Distribution". academia.edu.
8. ^ ^{a b c d} Barry C. Arnold (1983). Pareto Distributions. International Co-operative Publishing Business firm. ISBN978-0-89974-012-6.
9. ^ S. Hussain, S.H. Bhatti (2018). Parameter interpretation of Pareto distribution: Some modified moment estimators. Maejo International Journal of Science and Technology 12(1):11-27
10. ^ Eliazar, Iddo (Nov 2017). "Lindy's Law". Physica A: Statistical Mechanics and Its Applications. 486: 797–805. Bibcode:2017PhyA..486..797E. doi:ten.1016/j.physa.2017.05.077.
11. ^ ^{a b} Johnson NL, Kotz S, Balakrishnan Due north (1994) Continuous univariate distributions Vol 1. Wiley Series in Probability and Statistics.
12. ^ ^{a b c d} Johnson, Kotz, and Balakrishnan (1994), (twenty.4).
13. ^ Christian Kleiber & Samuel Kotz (2003). Statistical Size Distributions in Economics and Actuarial Sciences. Wiley. ISBN978-0-471-15064-0.
14. ^ ^{a b} Feller, W. (1971). An Introduction to Probability Theory and its Applications. Vol. Ii (2nd ed.). New York: Wiley. p. 50. "The densities (four.3) are sometimes called after the economist Pareto. It was thought (rather naïvely from a modernistic statistical standpoint) that income distributions should take a tail with a density ~ Ax ^−α as ten → ∞."
15. ^ Lomax, K. S. (1954). "Business organization failures. Another example of the assay of failure data". Journal of the American Statistical Association. 49 (268): 847–52. doi:10.1080/01621459.1954.10501239.
16. ^ Chotikapanich, Duangkamon (16 September 2008). "Chapter 7: Pareto and Generalized Pareto Distributions". Modeling Income Distributions and Lorenz Curves. pp. 121–22. ISBN9780387727967.
17. ^ White, Gentry (2006). Bayesian semiparametric spatial and joint spatio-temporal modeling (Thesis thesis). University of Missouri--Columbia. section five.3.1
18. ^ http://www.cs.bgu.ac.il/~mps042/invtransnote.htm
19. ^ ^{a b c d} Huang, Xiao-dong (2004). "A Multiscale Model for MPEG-four Varied Bit Rate Video Traffic". IEEE Transactions on Broadcasting. 50 (3): 323–334. doi:10.1109/TBC.2004.834013.
20. ^ Rootzén, Holger; Tajvidi, Nader (2006). "Multivariate generalized Pareto distributions". Bernoulli. 12 (five): 917–30. CiteSeerX10.1.ane.145.2991. doi:10.3150/bj/1161614952.
21. ^ M. E. J. Newman (2005). "Power laws, Pareto distributions and Zipf's law". Contemporary Physics. 46 (5): 323–51. arXiv:cond-mat/0412004. Bibcode:2005ConPh..46..323N. doi:ten.1080/00107510500052444. S2CID 202719165.
22. ^ H. J. Malik (1970). "Estimation of the Parameters of the Pareto Distribution". Metrika. fifteen: 126–132. doi:x.1007/BF02613565. S2CID 124007966.
23. ^ For a two-quantile population, where approximately eighteen% of the population owns 82% of the wealth, the Theil index takes the value 1.
24. ^ ^{a b c d e} Reed, William J.; et al. (2004). "The Double Pareto-Lognormal Distribution – A New Parametric Model for Size Distributions". Communications in Statistics – Theory and Methods. 33 (eight): 1733–53. CiteSeerX10.1.1.70.4555. doi:ten.1081/sta-120037438. S2CID 13906086.
25. ^ Reed, William J. (2002). "On the rank‐size distribution for human settlements". Periodical of Regional Scientific discipline. 42 (1): ane–17. doi:10.1111/1467-9787.00247. S2CID 154285730.
26. ^ Schroeder, Bianca; Damouras, Sotirios; Gill, Phillipa (2010-02-24). "Agreement latent sector error and how to protect against them" (PDF). 8th Usenix Briefing on File and Storage Technologies (FAST 2010) . Retrieved 2010-09-ten . We experimented with v different distributions (Geometric,Weibull, Rayleigh, Pareto, and Lognormal), that are normally used in the context of system reliability, and evaluated their fit through the full squared differences between the actual and hypothesized frequencies (χ² statistic). Nosotros establish consistently beyond all models that the geometric distribution is a poor fit, while the Pareto distribution provides the best fit.
27. ^ Yuji Ijiri; Simon, Herbert A. (May 1975). "Some Distributions Associated with Bose–Einstein Statistics". Proc. Natl. Acad. Sci. USA. 72 (5): 1654–57. Bibcode:1975PNAS...72.1654I. doi:x.1073/pnas.72.v.1654. PMC432601. PMID 16578724.
28. ^ Harchol-Balter, Mor; Downey, Allen (Baronial 1997). "Exploiting Process Lifetime Distributions for Dynamic Load Balancing" (PDF). ACM Transactions on Computer Systems. 15 (3): 253–258. doi:ten.1145/263326.263344. S2CID 52861447.
29. ^ Kleiber and Kotz (2003): p. 94.
30. ^ Seal, H. (1980). "Survival probabilities based on Pareto claim distributions". ASTIN Bulletin. 11: 61–71. doi:10.1017/S0515036100006620.
31. ^ CumFreq, software for cumulative frequency analysis and probability distribution fitting [1]
32. ^ Hardy, Michael (2010). "Pareto's Law". Mathematical Intelligencer. 32 (three): 38–43. doi:10.1007/s00283-010-9159-ii. S2CID 121797873.
33. ^ "62 people own the same as half the world, reveals Oxfam Davos report". Oxfam. Jan 2016.
34. ^ "Global Wealth Report 2013". Credit Suisse. Oct 2013. p. 22. Archived from the original on 2015-02-14. Retrieved 2016-01-24 .
35. ^ Tanizaki, Hisashi (2004). Computational Methods in Statistics and Econometrics. CRC Press. p. 133. ISBN9780824750886.

Notes [edit]

• M. O. Lorenz (1905). "Methods of measuring the concentration of wealth". Publications of the American Statistical Association. 9 (70): 209–19. Bibcode:1905PAmSA...ix..209L. doi:10.2307/2276207. JSTOR 2276207.
• Pareto, Vilfredo (1965). Librairie Droz (ed.). Ecrits sur la courbe de la répartition de la richesse. Œuvres complètes : T. III. p. 48. ISBN9782600040211.

• Pareto, Vilfredo (1895). "La legge della domanda". Giornale Degli Economisti. x: 59–68.
• Pareto, Vilfredo (1896). "Cours d'économie politique". doi:ten.1177/000271629700900314. S2CID 143528002.

External links [edit]

• "Pareto distribution", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Weisstein, Eric W. "Pareto distribution". MathWorld.
• Aabergé, Rolf (May 2005). "Gini'south Nuclear Family unit". International Conference to Honor Ii Eminent Social Scientists (PDF).

• Crovella, Marking E.; Bestavros, Azer (December 1997). Self-Similarity in World wide web Traffic: Prove and Possible Causes (PDF). IEEE/ACM Transactions on Networking. Vol. v. pp. 835–846. Archived from the original (PDF) on 2016-03-04. Retrieved 2019-02-25 .

• syntraf1.c is a C program to generate synthetic bundle traffic with bounded Pareto burst size and exponential interburst fourth dimension.

nelsontand1963.blogspot.com

Source: https://en.wikipedia.org/wiki/Pareto_distribution

Share this post